方差分析：穷人家的孩子学不好？

与统计和数据分析打交道的人，想必对方差分析一点都不陌生，但是真正懂得其原理的人又有多少呢？在写这篇文章之前，作为统计学专业毕业的人，表示对方差分析也只是一知半解，有时候还会出现误用的情况。为了写这篇文章，我又重拾《数理统计》这本书，经过一番推导和查阅相关资料后，总算是有了一定的了解。于是打算写这么一篇文章来与大家分享方差分析的原理以及用法，最后给出实际的例子。

1. 方差分析基本原理与思想

没有公式就没有伤害

为了不给大家造成伤害，我尽量不照搬公式，用人话来解释清楚。

方差分析的起源

一般两个样本的均值检验，现实中最常用的是t检验。因为t检验具有具有以下性质：

两总体方差未知时，可以使用；
非正态总体，大样本情况下可以使用；

而Z检验（又叫U检验）的前提条件就是两样本的总体方差已知，一般情况下总体的方差是不知道的，用样本的方差去估计个人认为偏差很大，所以Z建议现实生活中基本用不上。当然，如果你精通抽样技术（很难），能够计算无偏的总体方差估计，想必早就对这些基本方法不屑一顾了。

刚说了t检验只适用于两个样本的均值检验，那如果涉及到多个样本的均值检验呢？有人说:“两两t检验不就行了吗，虽然麻烦了一点，但还不是能做出来的，根本用不着新方法吧。”

假设有三个样本要对其均值进行检验是否相等，那么就要比较 $C_3^2 = 3$ 次了。关键问题是：若t检验的显著性水平 $\alpha = 0.05$ ,那么三次比较的显著性水平为 $1 - (1-\alpha)^3 = 0.1426$ ,远远超过当初的设定的0.05，犯第一类错误（弃真）概率大大加大。所以对于多样本的均值比较检验，应采用方差分析。

理论推导—以单因素方差分析为例

单因素方差分析是将影响试验结果的因素控制为1个，然后取该因素的几个水平进行分析。举个例子：现在要研究上网时间会不会影响学生的数学成绩？在同一个学校抽取成绩相当的90个学生，将其随机分为三组，每组30个学生。在一个月内，第一组控制每天不上网，第二组控制每天上网时间为1个小时，第三组控制每天上网时间为2个小时。三组在同一个班级上数学课，一个月后进行数学测试，对其结果进行方差分析。说了这么多就是将影响数学成绩控制为一个因素——上网时间。讲到统计学原理之类的东西，总是少不了公式，要不然会显得不够专业。但是考虑到大多数人看到公式就会直接略过，所以这部分结合例子一起来推导。

在公式推导前，先上一个表格，有助于对公式的理解。横轴A对应着3个水平，纵轴表示测试的学生个数r=30。得到数据如下表所示,一共有30行和3列：

水平	A1	A2	A3
1	$X_{11}$	$X_{12}$	$X_{13}$
2	$X_{21}$	$X_{22}$	$X_{23}$
3	$X_{31}$	$X_{32}$	$X_{33}$
…	$X_{…}$	$X_{…}$	$X_{…}$
r	$X_{r1}$	$X_{r2}$	$X_{r3}$
列平均值	$ \overline{X_{.1}}$	$ \overline{X_{.2}}$	$ \overline{X_{.3}}$

假设条件：
1. 三组的学生不受彼此影响，也就是样本的独立性；
2. 每个组内的学生考试成绩理论上服从 $N(\mu_j,\sigma^2)$ 的正态分布；
3. 方差齐性，也就是条件2里面相同的 $\sigma^2$ 。

这个假设是一切分析的基础，否则没法做下去了。令 $\varepsilon_{ij} = X_{ij} - u_j \sim N(0,\sigma^2)$ ,为随机误差； $\alpha_j = \mu_j - \mu$ , 其中 $\mu =\frac{1}{c} \sum \mu_j$ 为各水平的效应. 随机误差来源可能是学生发挥水平造成，当然也有其他各种各样的不可控原因。效应误差的来源是处理水平的不同——上网时间。当由处理水平不同造成误差在一定程度上大于由随机因素造成的误差的时候，我们就有理由认为是因为上网时间的不同导致学生考试成绩的差异。但是这个程度如何判断呢？这个就需要借助于F分布了。下面就是利用随机误差和效应误差的性质来推导出F分布，然后构成检验统计量用于判断。大波公式来袭，请注意 :)

这里方差分析的原假设为H0: $\mu_1=\mu_2 =\mu_3$ ; 备择假设为H1: $\mu_1,\mu_2 ,\mu_3$ 不全相等。

所有学生考试总偏差平方和为：

$SST = \sum{ \sum{ (X_{ij} - \overline{X_{..}})^2}} ,$

其中 $\overline{X_{..}} = \frac{\sum{\sum{X_{ij}}}}{n}$ 为90个学生的平均成绩。其可以分解为：

$SST = \sum{ \sum{ (X_{ij} - \overline{X_{.j}})^2}} + \sum{ r (\overline{X_{.j}} - \overline{X_{..}})^2}$

这就是平方和分解定理(证明过程感兴趣的可以看下面的参考文献1) 令： $SSE = \sum{ \sum{ (X_{ij} - \overline{X_{.j}})^2}}$ 为误差平方和， $SSA = \sum{ r (\overline{X_{.j}} - \overline{X_{..}})^2}$ 为水平的效应平方和。

从公式可以看出，误差平方和是先计算每个组的学生成绩与组的平均值的差值平方和，然后将所有组的加起来就是总的误差平方和；效应平方和是先计算每一个组均值减去所有组的均值的差值平方和，乘以组的学生个数，然后所有计算结果加起来就是总的效应平方和。

这个时候我们要用到了假设的部分，这部分需要知道基本统计分布的性质。拿第一列举例,j=1. 第一列的误差( $X_{i1} - \overline{X_{.1}}$ )是服从均值为0，标准差为 $\sigma$ 的正态分布 $\sim N(0,\sigma^2)$ , 那么这一列的误差平方和除以方差服从.

$\frac{\sum_{i=1}^{30}{ (X_{i1} - \overline{X_{.1}})^2}}{\sigma^2} \sim \chi^2(29)$

自由度为29的卡方分布。之所以要减去一个自由度是因为 $\overline{X_{.1}} = \frac{1}{30} \sum_{i=1}^{30}(X_{i1})$ ，利用了样本信息，故丢失一个自由度。由于卡方分布的可加性，那么所有列的误差平方和

$\frac{SSE}{\sigma^2} \sim \chi^2(n - 3) ,其中 n=90 .$

因为卡方分布的期望是其自由度，可以知道SSE的期望是

$\frac{E(SSE)}{n-3} = \sigma^2$

当H0为真时， $X_{ij} \sim N(\mu,\sigma^2).$

$\therefore \frac{SST}{\sigma^2} = \frac{\sum{ \sum{ (X_{ij} - \overline{X_{..}})^2}}}{\sigma^2} \sim \chi^2(n-1)$

由分解定理可知:

$\frac{SSA}{\sigma^2} = \frac{\sum_{i=1}^{r}{ (X_{.j} - \overline{X_{..}})^2}}{\sigma^2} \sim \chi^2(3 - 1)$

可以求得：

$\frac{E(SSA)}{2} = \sigma^2$

当H1为真时，计算得：

$E(SSA) = 2 \times \sigma^2 + \sum_{j=1}^{c}r\alpha_j^2$

其值跟 $\alpha_j$ 水平的效应有关系，水平效应越大，则实际的SSA越大(推导请见参考资料1)。而SSE不管H0是否为真, $E(SSE) =(n-3) \sigma^2$ 。

F分布是由两个卡方分布分别除以其自由度的比值构成的，当H0为真时，以SSE/(N-3)作为分母，以SSA/(3-1)作为分子就可以可以构建*检验统计量F。 F分布见文章标题的底图。

$F = \frac{SSA/(3-1)}{SSE/(N-3)} \sim F(2,87)$

结果判断

检验统计量F的计算是基于实际样本的观测值计算的，若试验水平的效应很小，则F值小；若水平的效应很大，则F值大。

统计学上，小概率事件(在一次实验中看成是实际不可能发生的事件)，一般认为其发生的概率等于或小于0.05或0.01。若发生小概率事件发生，则认为其在统计学上具有显著性。
基于给定的显著水平 $\alpha=0.05$ ，本题的拒绝域为：

$F \ge F_{0.05}(2,87)$

若计算的F值大于或等于 $F_{\alpha}(2,87)$ ，即落在了拒绝域中，所以可以拒绝原假设，认为各水平的均值不相等。若计算出来的F值小于 $F_{\alpha}(2,87)$ ，则没有充分的理由认为是上网时间影响学生成绩，不具有统计上的显著性。

$F_{0.05}(2,87)$ 一般需要查表才知道其值，但是P值的出现解决了查表比对的问题。在H0为真的情况下，设计算的统计量值为F0，则 $p_{value} = P \{ F \ge F_0 \}$ 。实际上P值可以理解为尾部概率，若尾部概率越小，F值越大，试验的水平效应越大，越应该拒绝原假设。当P值接近临界值(给定的显著性水平)，不能武断做出推断。例如P=0.052时，略大于给定的显著性水平0.05，这种情况下如果条件允许可以多做几次试验，综合实际情况给出判断。

方差分析的思想

上面推导了单因素方差分析的基本原理，但是实际问题中我们还会碰到多因素以及因素之间的交互作用的情况，其基本的思想是一致的：就是将每一个因素造成的误差给分解出来，分别与随机误差进行比较。本例中将学生成绩的差异来源分解成了随机误差和效应误差（其实效应误差是含有随机误差的，见参考资料1的P23），当效应误差大于一定的随机误差时，可以认为引起差异的原因大部分在于水平变量的控制。F分布解决了如何判断问题，它是由英国统计学家R.A.Fisher提出，并以其姓氏的第一个字母命名的。Fisher是现代统计学奠基人之一。方差分析一般的结果呈现是方差分析表的形式：

方差来源	平方和	自由度	均方	F比值	p值
因素A	SSA	R-1	MSA=SSA/(R-1)	FA= MSA/MSE
因素B	SSB	S-1	MSA=SSB/(S-1)	FB= MSB/MSE
…	…	…	…	…	…
误差	SSE	(R-1)(S-1)	MSE=SSE/(R-1)(S-1)
总合	SST	RS-1

请牢记方差分析的假设条件：1.各组样本独立；2.组内误差服从正态分布；3.各组间的方差近似相等。

前面两个条件一般都比较好满足，最后一个同方差性比较难满足。很多人在做方差分析前都没有对样本进行检验，拿起数据就算，这样得出的结果是不可信的。有人会问如果条件都不满足，那怎么办? 我的建议是可以尝试非参数的方法，比如kruskal-wallis单因素方差分析，Friedman秩方差分析法。下面介绍一个完整的方差分析的步骤，并给出实例。

2. 实例分析

这里我们研究的问题是：处在不同经济水平地区的学校学生的平均成绩是否有差异。我们是用学校周边的房价来衡量经济水平的高低，并将学校分为三挡。平均成绩用2014年各学科各年级的平均成绩。

本人使用的是R软件，软件只是思想的载体，方差分析的思路都是一致。下面请看完整的方差分析过程。

首先载入需要packages，准备好数据：

library(readxl)
library(dplyr)
library(ggplot2)
a <- read_excel("data.xlsx") #导入数据
Source: local data frame [84 x 5]
    xxdm   eco      chi      mat      eng
   (chr) (chr)    (dbl)    (dbl)    (dbl)
1   0003    高 86.63555 84.55955 84.69365
2   0004    高 82.80060 84.32115 79.51330
3   0007    高 85.01712 86.03630 88.01676
4   0008    高 81.89492 82.90956 84.15971
5   0009    高 85.50658 85.68337 89.13135
6   0010    高 83.41341 85.41472 84.65958
7   0012    高 81.03484 80.36919 85.29970
8   0015    高 84.27045 88.00999 88.32905
9   0024    高 80.03031 79.97170 79.62687
10  0039    高 84.38389 87.05825 85.93709
...  ...   ...      ...      ...      ...

这就是基本的数据的样子，xxdm表示学校代码；eco表示经济水平，有高中低三个档；chi表示语文平均成绩，mat表示数学平均成绩，eng表示英语平均成绩。

经济水平与语文平均成绩

首先通过箱线图来了解，处在不同经济水平的学校语文平均成绩总体情况：

windowsFonts(myfont=windowsFont("Microsoft YaHei")) # 绑定字体-微软雅黑
p <- ggplot(a, aes(eco,chi,colour=factor(eco)))
p + geom_boxplot(colour= "darkgrey",outlier.colour = "red", 
		outlier.shape = 2,outlier.size = 3) +  #设置箱体颜色标出离群点
  geom_jitter(width = 0.2,size=3) +  #散点分布
  coord_flip() +  #坐标轴翻转
  labs(y="各学校平均成绩",x="经济水平",colour="经济水平") +  #坐标轴及标题
  ggtitle("不同经济水平下学校语文平均成绩箱线图")+
  theme_bw()+  #简洁主题，设置标题字体
  theme(plot.title=element_text(family = "myfont",face = "bold",size=rel(2)),
        axis.title.x=element_text(family = "myfont",face = "bold"),
        axis.title.y=element_text(family = "myfont",face = "bold"),
        legend.title=element_text(family = "myfont",face = "bold"))

得到的图是这样的：
不同经济水平下学校语文平均成绩箱线图

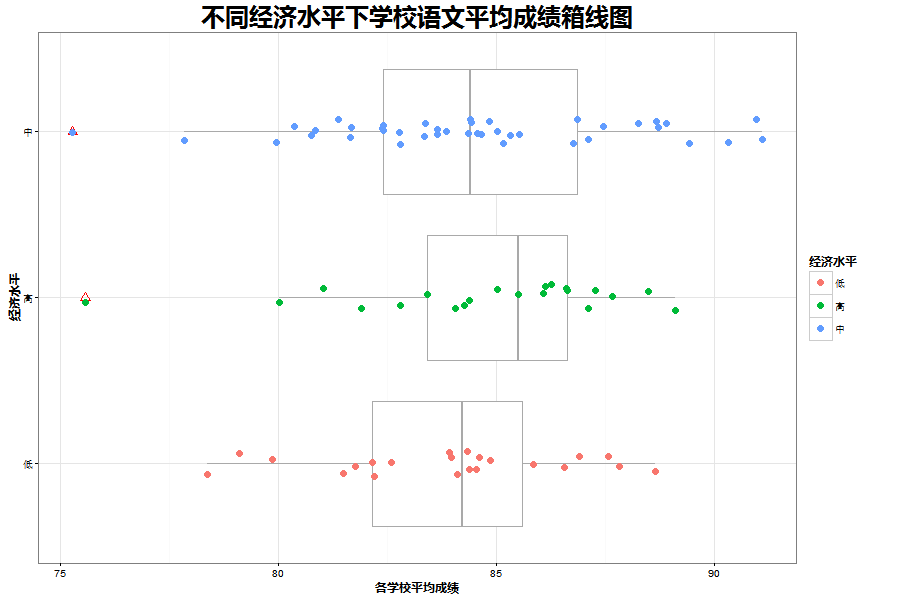
从上面的图可以看出有中等经济水平和高经济水平各有一个学校为离群点，为了准确性，应该剔除这两个学校。在数据准备好的情况下，就可以进行分析前的检验。所以，这里的水平有3个，样本数量为82个。

正态性检验

#剔除异常值并将语文成绩排序
>chinese <- select(a,c(1:3)) %>% filter(chi>76) %>% arrange(chi)
Source: local data frame [82 x 3]
    xxdm   eco      chi
   (chr) (chr)    (dbl)
1   1032    中 77.84325
2   0038    低 78.36574
3   0029    低 79.11266
4   0030    低 79.87137
5   1008    中 79.94627
6   0024    高 80.03031
7   0042    中 80.36948
8   0025    中 80.76178
9   0046    中 80.85167
10  0012    高 81.03484
..   ...   ...      ...
#低经济水平学校正态性检验
>shapiro.test(filter(chinese,eco =="低") %>% select(chi) %>% .[[1]])

	Shapiro-Wilk normality test
data:  filter(chinese, eco == "低") %>% select(chi) %>% .[[1]]
W = 0.97135, p-value = 0.7422

> shapiro.test(filter(chinese,eco =="中") %>% select(chi) %>% .[[1]])

	Shapiro-Wilk normality test
data:  filter(chinese, eco == "中") %>% select(chi) %>% .[[1]]
W = 0.97593, p-value = 0.5417

> shapiro.test(filter(chinese,eco =="高") %>% select(chi) %>% .[[1]])

	Shapiro-Wilk normality test
data:  filter(chinese, eco == "高") %>% select(chi) %>% .[[1]]
W = 0.96808, p-value = 0.7139

可以看到三个水平下学校的平均成绩正态性检验结果P值都较大，可以认为满足正态性。

方差齐性检验

多组的方差齐性检验采用 Bartlett Test of Homogeneity of Variances，其H0为每组方差相等。

>bartlett.test(chi ~ eco, data=chinese)

	Bartlett test of homogeneity of variances
	
data:  chi by eco
Bartlett's K-squared = 1.8056, df = 2, p-value = 0.4054.

通过P值发现并不能拒绝H0，可以认为样本的方差是齐性的，符合方差分析的条件。

方差分析

>c.aov <-aov(chi~eco,data=chinese)
> summary(aov(chi~eco,data=chinese))

            Df Sum Sq Mean Sq F value Pr(>F)
eco          2   18.3   9.132    1.07  0.348
Residuals   79  674.1   8.533

看到这个结果是不是很熟悉，这个就是前面方差分析表。通过查看P值，远大于显著性水平0.05，所以不能拒绝原假设，认为不同经济水平对学校的语文平均成绩没有显著性影响。

经济水平与数学平均成绩

步骤与上面分析语文平均成绩类似，有些代码省略。首先通过箱线图来了解，处在不同经济水平的学校数学平均成绩总体情况.得到的图是这样的：

不同经济水平下学校数学平均成绩箱线图

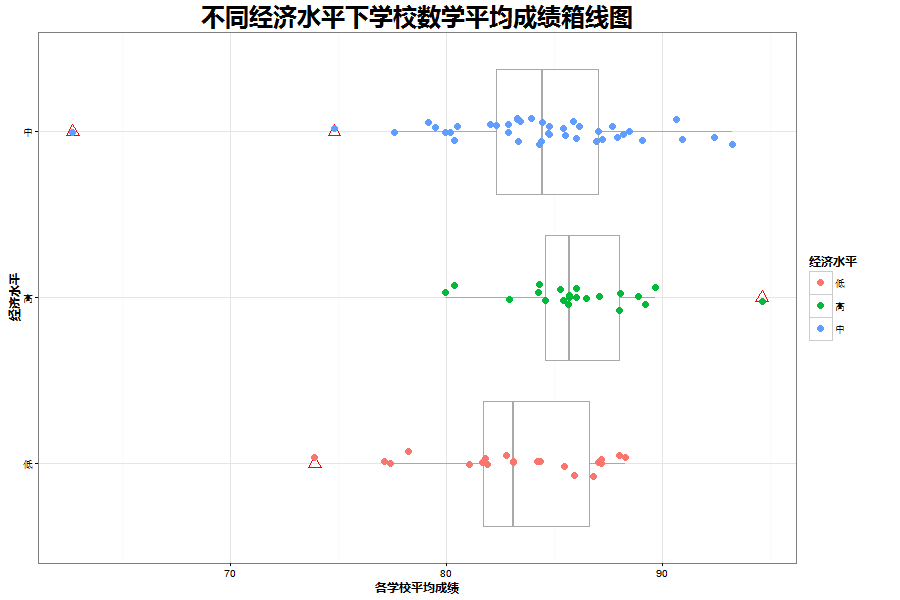
数学的箱线图中有一个异常点非常明显应该剔除掉。剔除后得到的图是这样的：

剔除异常值后数学的箱线图

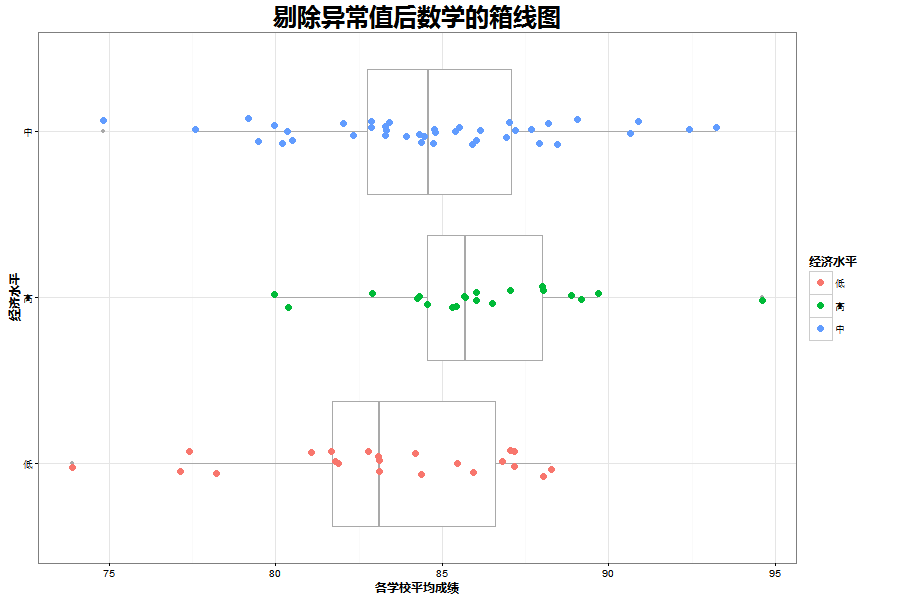
相比语文的箱线图，不同水平下的数学均值差异略大一些。接下来需要方差分析来验证一下。

正态性检验

> shapiro.test(filter(math,eco =="低") %>% select(mat) %>% .[[1]])

	Shapiro-Wilk normality test

data:  filter(math, eco == "低") %>% select(mat) %>% .[[1]]
W = 0.93386, p-value = 0.1476

> shapiro.test(filter(math,eco =="中") %>% select(mat) %>% .[[1]])

	Shapiro-Wilk normality test

data:  filter(math, eco == "中") %>% select(mat) %>% .[[1]]
W = 0.99041, p-value = 0.9794

> shapiro.test(filter(math,eco =="高") %>% select(mat) %>% .[[1]])

	Shapiro-Wilk normality test

data:  filter(math, eco == "高") %>% select(mat) %>% .[[1]]
W = 0.94347, p-value = 0.255

中等水平下的学校平均成绩更加符合正态分布，其他两个水平勉强服从总体分布。

方差齐性检验

> bartlett.test(mat ~ eco, data=math)

	Bartlett test of homogeneity of variances

data:  mat by eco
Bartlett's K-squared = 1.2086, df = 2, p-value = 0.5465

方差齐性也通过检验，下面可以进行方差分析。

方差分析

> summary(aov(mat~eco,data=math))

            Df Sum Sq Mean Sq F value Pr(>F)  
eco          2   92.4   46.22   3.293 0.0423 *
Residuals   80 1122.9   14.04                 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

在0.05显著性水平，可以认为经济水平会影响到数学的平均成绩。

经济水平与英语平均成绩

原始数据：

Source: local data frame [84 x 3]

    xxdm   eco      eng
   (chr) (chr)    (dbl)
1   1008    中 71.47867
2   1020    中 72.24419
3   0038    低 72.27352
4   1030    低 72.91755
5   0030    低 75.05625
6   4006    低 78.20742
7   5001    中 79.12962
8   0004    高 79.51330
9   0024    高 79.62687
10  1032    中 79.74482
..   ...   ...      ...

首先通过箱线图来了解，处在不同经济水平的学校英语平均成绩总体情况.得到的图是这样的：

不同经济水平下学校英语平均成绩箱线图

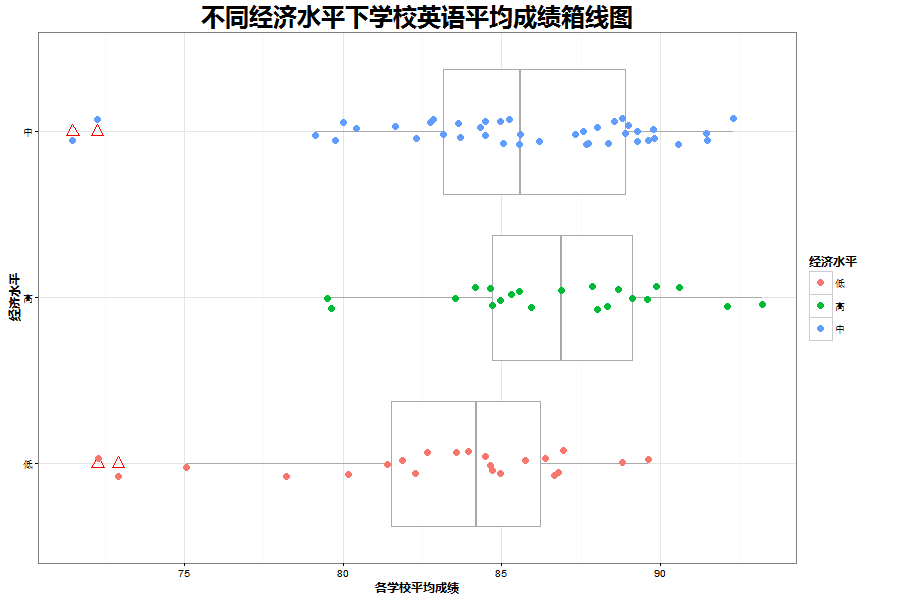
英语的箱线图中有四个异常点非常明显，特别是处在中等经济水平的学校。先尝试去掉四个点，后尝试只去掉中等水平下的两个点。

正态性检验

> eng <- select(a,c(1,2,5)) %>% arrange(eng) %>% filter(eng>73)
> shapiro.test(filter(eng,eco =="低") %>% select(eng) %>% .[[1]])

	Shapiro-Wilk normality test

data:  filter(eng, eco == "低") %>% select(eng) %>% .[[1]]
W = 0.95912, p-value = 0.5265

> shapiro.test(filter(eng,eco =="中") %>% select(eng) %>% .[[1]])

	Shapiro-Wilk normality test

data:  filter(eng, eco == "中") %>% select(eng) %>% .[[1]]
W = 0.96591, p-value = 0.2791

> shapiro.test(filter(eng,eco =="高") %>% select(eng) %>% .[[1]])

	Shapiro-Wilk normality test

data:  filter(eng, eco == "高") %>% select(eng) %>% .[[1]]
W = 0.9679, p-value = 0.6862

可以认为通过了正态性检验。

方差齐性检验

> bartlett.test(eng ~ eco, data=eng)

	Bartlett test of homogeneity of variances

data:  eng by eco
Bartlett's K-squared = 0.0060188, df = 2, p-value = 0.997

方差齐性也通过检验，下面可以进行方差分析。

> summary(aov(eng~eco,data=eng))

            Df Sum Sq Mean Sq F value Pr(>F)  
eco          2   93.9   46.97   3.775 0.0273 *
Residuals   77  958.1   12.44                 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

在0.05显著性水平下，可以认为经济水平显著性地影响英语的平均成绩。

现在考虑第二种情况，因为中等经济水平的那两个异常值离最小值非常远，而低经济水平两个异常值离最小值相对较近，可以考虑只去掉两个值。

> summary(aov(eng~eco,data=eng1))

            Df Sum Sq Mean Sq F value  Pr(>F)   
eco          2  198.6   99.29   6.577 0.00228 **
Residuals   79 1192.6   15.10                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

从结果来看，经济水平对英语平均成绩的影响非常的显著。总的来说，在三个科目中，经济水平对英语平均成绩影响最大，其次是数学平均成绩，语文平均成绩可以认为没有影响。

3. 结语

这篇文章从详细的解释了方差分析的基本原理，并在后面给出了实例分析，有助于加深对方法分析的理解，避免在今后的使用各种犯错误。当然，关于后的实例，还可以进一步深入分析各个年级的平均成绩与经济水平之间的关系。读者可以自行去深入去研究，另外文章给出的代码都是可以复用的。

4. 参考文献

[1]关于方差分析的详细推导请看这里：四川大学唐嗣政教授手稿P20-P28

Bruce Zhao / 2016-01-15
Published under(CC) BY-NC-SA 3.0 CN.

水平	A1	A2	A3
1	\(X_{11}\)	\(X_{12}\)	\(X_{13}\)
2	\(X_{21}\)	\(X_{22}\)	\(X_{23}\)
3	\(X_{31}\)	\(X_{32}\)	\(X_{33}\)
…	\(X_{…}\)	\(X_{…}\)	\(X_{…}\)
r	\(X_{r1}\)	\(X_{r2}\)	\(X_{r3}\)
列平均值	\( \overline{X_{.1}}\)	\( \overline{X_{.2}}\)	\( \overline{X_{.3}}\)

方差分析：穷人家的孩子学不好？

重新认识方差分析

目录

1. 方差分析基本原理与思想

方差分析的起源

理论推导—以单因素方差分析为例

结果判断

方差分析的思想

2. 实例分析

经济水平与语文平均成绩

正态性检验

方差齐性检验

方差分析

经济水平与数学平均成绩

正态性检验

方差齐性检验

方差分析

经济水平与英语平均成绩

正态性检验

方差齐性检验

3. 结语

4. 参考文献