随着信息科技的高速发展,互联网让人与人之间的通信成本不断降低,同时通信效率不断提升。在这一浪潮下,传统的发收问卷的形式瞬间有所改善,让问卷的发生和回收更为高效。
于是乎,各行各业的问卷数据呈现蓬勃发展的趋势,尤其是QQ这种互联网大佬,动不动就让你填个调查问卷什么的。当然也有良心企业如,问卷星。
已经完全跑题了,也不补救了,反正今天的话题和问卷多少有点关系。是关于多个评分者打分一致性的问题。以下进入正文。
一致性与相关性
在具体讲算法之前,我们需要先对一致性和相关性的概念加以区分,为什么这么说呢?因为在很多时候,我们在一致性分析的时候通常不会考虑太多,直接采用相关系数的方法进行计算,那么这种做法对不对呢?
其实不能算全错,而是在有些条件下并不适用。可以先看看以下图表。
这里模拟了两位评价者对6名被试的打分情况,分值区间为0-100:
| 被评价者 | 评分者A | 评分者B |
|---|---|---|
| 样本1 | 10 | 80 |
| 样本2 | 11 | 81 |
| 样本3 | 12 | 82 |
| 样本4 | 13 | 83 |
| 样本5 | 14 | 84 |
| 样本6 | 15 | 85 |
如果按照相关的方法,有且仅有两个对象情况下,我们可以使用散点图的形式表达,如下:
图1 评分者散点图在这种情况下:R²=1 !!!
是啊,这两个评分者在这个图形上的所有点都落在了一条直线上。但是,似乎有什么不对?
那就再看看下一个图。
图2 评分者柱状图是不是突然有种沃德法克的感觉?
实际上,这两位只是对不同样本的好坏评价程度比较一致,但是在打分的严格程度方面,完全不一样啊。
评价者A典型的“目中无人”,大约他的心理独白是:就你们这群战斗力只有5的渣渣,不打0分己经很给面子了好么?
评价者B就是典型的“中国式打分砖家”,大约他的心理独白是:100分啊,那就给个80分左右吧。
所以,上面说了一大摞,只是单纯地想告诉大家一个事实:相关性和一致性是不一样的。
相关性通常应用在不同量纲、不同单位的数据中,比如身高和体重。
一致性则用于在所有其他条件均相同,仅参与评价的人员不同的情况下。
那么,不同评分者之间应该采用何种统计方法计算其一致性呢?
推荐这样一张表(具体见Reference)
总体而言,0,1变量就考虑Kappa;等级变量考虑Kendall或者加权Kappa;连续变量则考虑ICC
绕了半天,故事的主角ICC终于出现了,以下浸入正片环节。
ICC概念
ICC的全称是intraclass correlation coefficient,即组内相关系数。有好事的小伙伴肯定又要吐槽了:这不还是相关系数吗???
此处我只能偷偷告诉你,对啊,就是相关系数,但是不是相关性啊。而且,它叫组内相关系数。
一般到这里都会用公式解释ICC和普通的相关系数(一般是pearson)的区别,但是作为坚决不爱贴公式的人,我推荐把文章拉到底,点Reference下的第二个链接。
实际上,要理解ICC关键在于,首先你要确定你的研究对象的性质。先引用一段:
选择恰当的ICC取决于 以下三个方面:(1)所选的模型是one-way model或two-way model;(2)选择single measure或average measure;(3)选择absolute agreement或consistency。
如果用SPSS的话,这三个选项都是不可避免的:
实际上,ICC使用并不那么艰难,但是在理解这三个概念上要花费大量的时间。
因此,我根据我在操作中的实际经验简单讲一下。
- one-way or two-way?
one-way是单因素随机效应模型,即单因素方差模型,其自变量为每个样本,因变量为得分。整体上,这个方式适用于【每个被试者由不同的随机选择的评定者评分】或【所有被试者由一个评定者评分】。
two-way是双因素随机效应模型,即双因素方差模型,其自变量为每个样本以及不同的评价者,因变量为得分。整体上,这个方式适用于【重测信度】或【多评分者的一致性】。
另外,补充一点:two-way模型分为随机效应(random)和混合效应(mixed),前者计算的结果可推广到所有可能的评定者,后者仅限于当前的评分者不可推广。 - single measure or average measure?
single measure分析单个评分者评分的可靠性。
average measure则使用了多个评分者的均值进行可靠性研究。在双因素模型中的average measure ICC等于Cronbach's α系数 - absolute agreement or consistency?
absolute agreement是考虑了不同评定者存在不同的系统误差,也即评分者之间打分的严格程度并不一致。
consistency是认为不同评分者水平一致的一致性系数计算方式,不考虑由不同评分者自身带来的系统误差。
最后,ICC的区间是[0,1],所以,有人建议ICC大于0.80为高度一致、0.61-0.80为中等,0.41-0.60为一般,0.11-0.40为较低,小于0.1为无一致性。
ICC应用
我知道的,不拿点干货出来是没法让大家满足的。而且,老实说,上文的内容比较枯燥乏味。
所以,我这里结合具体的项目研究来展开。项目背景就是一次对不同学校的评分。其中有两项是相同的两个评价者在不同指标上的评价结果。这里使用的统计软件是SPSS。
首先,数据录入。就不多讲了。
然后,点击【分析】-【度量】-【可靠性分析】,选择变量后点击【统计量】,勾选【同类相关系数】,模型使用【双向随机】,类型为【绝对一致】,如下图
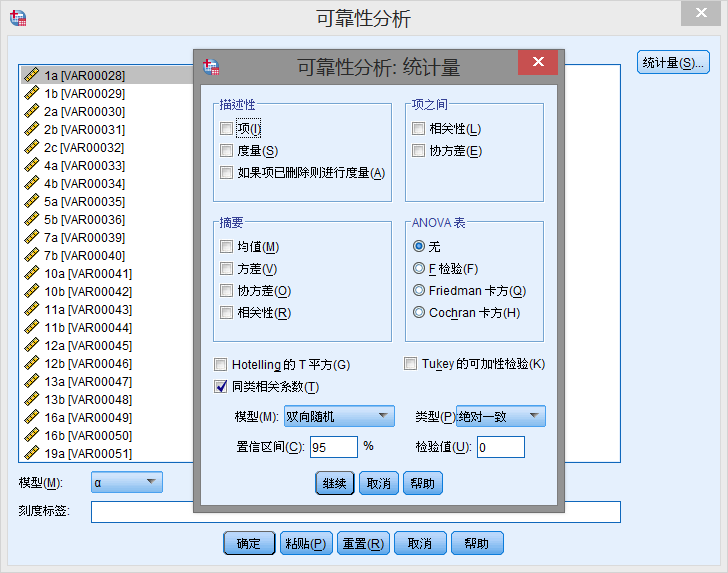
点击【继续】、选择需要统计的变量,点击【确定】,即刻呈现结果:
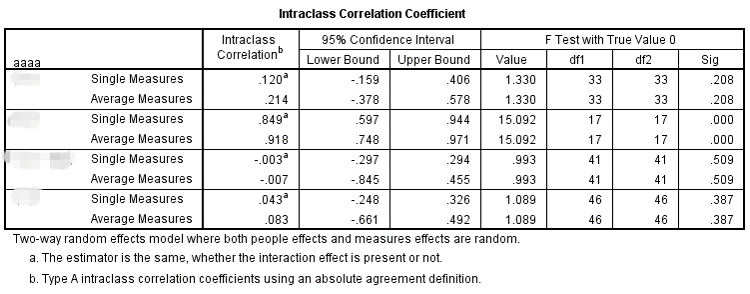
简单的解读下结果,可以看到这个两个变量在不同的分组内出现了不同的结果,在第一、第三和第四个组的一致性非常低,并且没有达到统计上的显著水平(p>0.05);仅第二组的一致性稍高,也达到统计上的显著水平(p<0.05)。所以,除了第二组外,其他几组的评分者一致性都存在疑问。
当然,教完你们用这个工具还没完,上文提到了,是相同评价者在不同指标的评价结果,所以,有趣的结论就出现了:
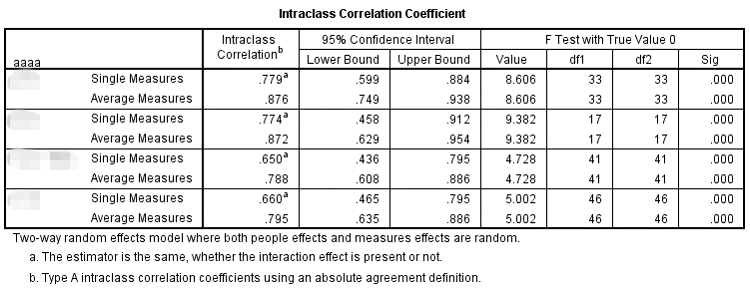
这个指标上,两个相同的评价者在不同的组别间均出现了较高的一致性,也都达到了统计上的显著水平(p<0.05)。
简单来说,就是某一专家小组的两位成员在一个方面达成了共识,但是另一个方面出现了较大的分歧。那么究竟是什么原因导致了这一结果呢?值得深思啊...
结束语:
大体上,这一期和大家分享了关于一致性的计算和研究。当然,并不能说文章就无懈可击了,依然还有很多值得深入研究的地方,毕竟在文章分的副标题上可是放了一个“概化理论”的头衔。那玩意儿可是在评分者一致性研究领域中的一朵大(qi)咖(pa)。所以,如果要深入研究,不妨可以考虑往这个方向。
另外,在一致性的研究中,Rwg也是个课题,就不作为这一期的主要内容了。
回过头来,仔细思考之前做的一些统计研究,其实还存在着很多并不完善的地方。并不是那些都是错的,只能说是不够准确,但是,不能一直将错就错下去了,不断地学习和自我纠正才是成长的标志。毕竟,这辈子,不犯错还能称之为“人类”么?
Reference
豆丁网:一致性检验方法的合理应用
百度文库:组内相关系数及其软件实现
豆丁网:ICC值在量表信度分析中的应用